Monty Hall paradoksu
Monty Hall paradoksu adını bir zamanların populyar televiziya şousu “Let’s Make A Deal”in aparıcısı Monty Hall-dan götürüb. Məsələnin qoyuluşu isə belədir:
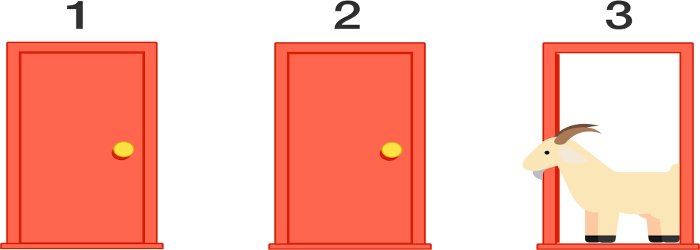
- Üç qapı var
- Qapılardan yalnız birinin arxasında böyük priz var, digər ikisi boşdur
- Aparıcı başlanğıcda sizdən bir qapı seçməyinizi xahiş edir, amma həmin qapını açmır
- Geriyə iki qapı qalır və aparıcı onlardan birini (hədiyyə olmayanı) açıb göstərir
- Və sizdən soruşur: ilk seçdiyiniz qapını açım, yoxsa fikrinizi dəyişib digər qapını açdırmaq istəyirsiniz?
Sizcə fikrinizi dəyişməklə dəyişməmək arasında qazanmaq ehtimalınız baxımından bir fərq varmı? Əksəriyyət düşünür ki, heç bir fərq yoxdur. Amma əslində fikrinizi dəyişməklə prizi udma ehtimalınız 2 dəfə artır! İntuisiyaya zidd səslənsə də riyazi olaraq isbatı var. Necə?
Başlanğıc sadədir. Üç qapı var, və hədiyyənin hər birinin arxasında olma ehtimalı 1/3-dür.
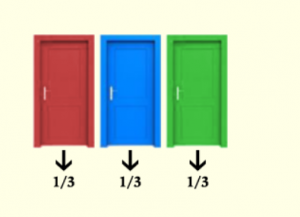
Tutaq ki, biz əvvəldə qırmızı qapını seçmişik. Aparıcı yaşıl qapını açıb sizə göstərir ki, onun arxasında priz yoxdur. Belə olan halda qırmızı qapının uduşlu olması ehtimalı dəyişmir, əvvəlki kimi 1/3 olaraq qalır. İndi yaşıl qapı açılıb və yerdə qırmızı və göy qapılar qalıb. Yuxarıda dediyimiz kimi, qırmızı qapının ehtimalı 1/3 olaraq qalır. Amma digər tərəfdən də ehtimalların cəmi 1-ə bərabər olmalıdır. Bu isə, prizin digər qapının (bu nümunədə göy qapının) arxasında olma ehtimalını 2/3 edir.

Məntiqə sığmasa da bu faktdır və tam riyazi isbata bu linkdən baxa bilərsiniz: https://www3.nd.edu/~jstiver/Exec_Micro/Monty%20Hall.pdf
Aşağıdakı videoda hər iki ssenarini Python-da simulyasiya edərək nəticələri nümayiş etdirəcəyik. Siz də Python-u yükləyərək mənimlə birgə bunu edə bilərsiniz (yazının sonunda yükləmək üçün instruksiyalar verilib). Gəlin riyaziyyatın gözəlliklərini birlikdə kəşf edək.
Anacondanı yükləmək üçün instruksiya: https://problemsolvingwithpython.com/01-Orientation/01.03-Installing-Anaconda-on-Windows/
Python kodu:
#!/usr/bin/env python # coding: utf-8 # In[1]: import numpy as np import pandas as pd import random from random import randint import matplotlib.pyplot as plt # In[17]: simulyasiya_sayi=1000 toplam_udushlu_oyunlarin_sayi_1=0 faiz=np.array([]) for i in range(0, simulyasiya_sayi): qapilar=[1,2,3] udushlu_qapi=randint(1,3) ishtirakchinin_ilk_sechdiyi_qapi=randint(1,3) qapilar.remove(udushlu_qapi) if ishtirakchinin_ilk_sechdiyi_qapi != udushlu_qapi: qapilar.remove(ishtirakchinin_ilk_sechdiyi_qapi) aparicinin_achdigi_qapi=random.choice(qapilar) #oyunchu ilk sechdiyi qapini achdirir if ishtirakchinin_ilk_sechdiyi_qapi == udushlu_qapi: toplam_udushlu_oyunlarin_sayi_1=toplam_udushlu_oyunlarin_sayi_1+1 faiz=np.append(faiz, toplam_udushlu_oyunlarin_sayi_1/(i+1)) # In[18]: toplam_udushlu_oyunlarin_sayi_1 # In[25]: simulyasiya_sayi=1000 toplam_udushlu_oyunlarin_sayi_2=0 faiz=np.array([]) for i in range(0, simulyasiya_sayi): udushlu_qapi=randint(1,3) ishtirakchinin_ilk_sechdiyi_qapi=randint(1,3) qapilar=[1,2,3] qapilar.remove(udushlu_qapi) if ishtirakchinin_ilk_sechdiyi_qapi != udushlu_qapi: qapilar.remove(ishtirakchinin_ilk_sechdiyi_qapi) aparicinin_achdigi_qapi=random.choice(qapilar) #oyunchu fikrini deyishib, diger qapini achdirir qapilar=[1,2,3] qapilar.remove(aparicinin_achdigi_qapi) qapilar.remove(ishtirakchinin_ilk_sechdiyi_qapi) ishtirakchinin_sechdiyi_yeni_qapi=qapilar[0] if ishtirakchinin_sechdiyi_yeni_qapi==udushlu_qapi: toplam_udushlu_oyunlarin_sayi_2=toplam_udushlu_oyunlarin_sayi_2+1 faiz=np.append(faiz,toplam_udushlu_oyunlarin_sayi_2/(i+1) ) # In[26]: toplam_udushlu_oyunlarin_sayi_2 # In[11]: faiz=pd.Series(faiz) axes=plt.gca() axes.set_ylim([0,1]) axes.set_xlim([0,simulyasiya_sayi]) faiz.plot() plt.show() # In[29]: faiz=pd.Series(faiz) axes=plt.gca() axes.set_ylim([0,1]) axes.set_xlim([0,simulyasiya_sayi]) faiz.plot() plt.show()